8 皇后问题
related link: https://zhuanlan.zhihu.com/p/99209213
8皇后问题是经典的递归回溯问题. 最主要的是理解回溯算法的思想. 上面的知乎专栏的老哥讲的有点啰嗦, 核心部分我自己也没看懂, 所以自己实现了一版Go语言版本. 并还是会简单讲一下算法实现. 开工之前, 还是先看看题目.
题目
8*8 的棋盘上要摆放8个皇后, 每个皇后以自己为中心, 彼此之间米字型的射线范围内不能相遇, 求有多少种摆放方式.
分析
其实不用绕弯子, 紧紧围绕递归和回溯来解决问题就好了. 我一开始是纵向来考虑问题的, 也就是一列一列的去放, 但是看了专栏和其他的博客, 普遍是按行处理的, 符合数组通常是按行存储的, 其实都可以, 为了保持一致, 这里也是按行处理.
既然涉及到递归, 先要考虑清楚递归体里做了什么:
- 在一个新的行中从左到右依次尝试在列上放一个皇后;
-
检查该皇后是不是和之前上面的行中已经放好皇后米字型相遇;
2.1 如果相遇, 则说明这次尝试放皇后的位置不正确, 取消放置当前位置, 并尝试放到下一个位置(列);
2.2 如果没有相遇, 说明这个位置合法, 此时表示可以进行下一行(这里就是向下递归了);
- 如果向下递归了, 那么不论下游的结果如何, 自己也会在递归结束后将当前行的皇后移除, 并尝试放到下一个位置(列), 和2.1做的事情一样.
- 如果整列都没有匹配,则说明上一行或者多行的排列结果不满足要求, 于是回到上一行尝试上一行皇后的其他摆放位置, 进行
1,2的操作 - 当递归到第9行时(当然不存在第9行), 说明前8行都已经放好了皇后, 此时说明一种摆放策略已经成功了, 于是计数器加一并输出结果.
其中, 1-3都是递归的循环体, 4,5是递归的返回体. 而这里的回溯则体现在4.中. 后面看到代码时再说.
这里尝试以图说明:
向下递归过程
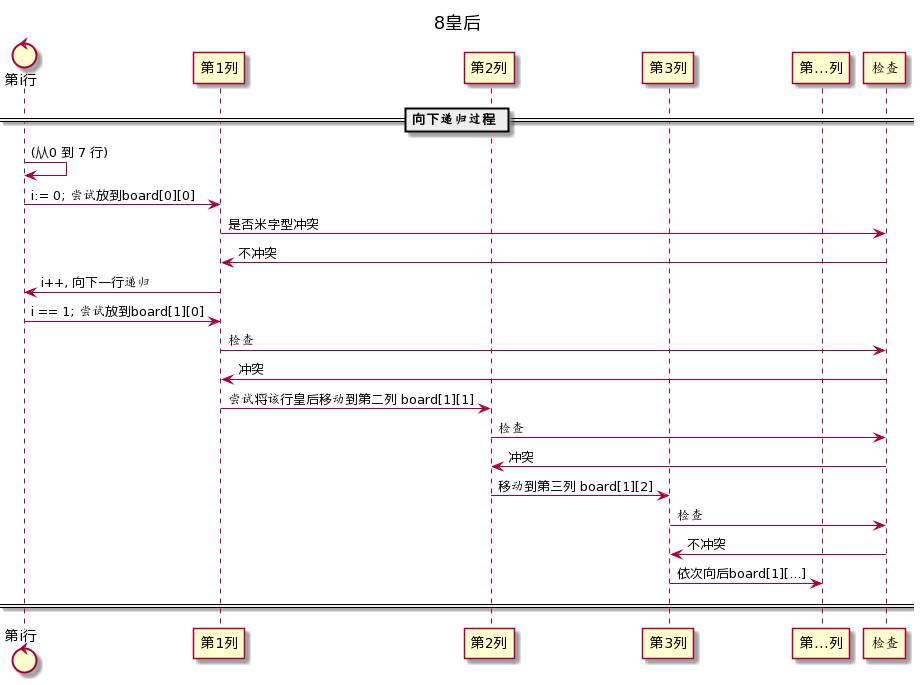
注意上图中, i++的时候其实是到下一行了, 行与列要仔细区别一下.
向下递归看完了可以在看看向上回退的情形.
向上回退情形1: 该列找不到合适的位置放置新皇后
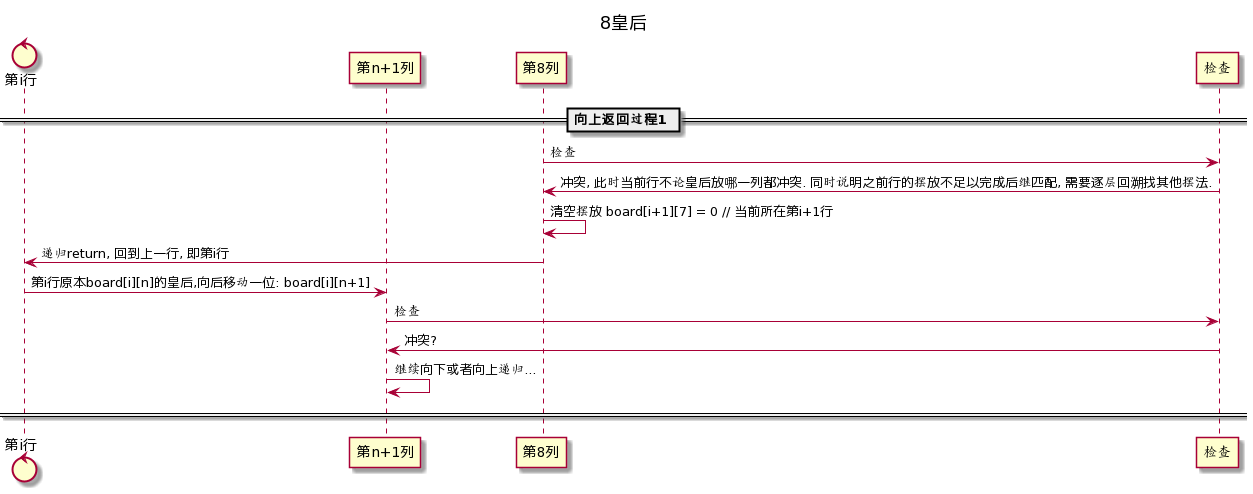在这种情形下, 由于新的一列所有位置都会和已有的皇后们冲突, 无法放到任何位置上了, 因此这一行不能放任何皇后, 并且至少上一行, 也可能是多行的皇后摆放都是不可以的, 因此要向上回退尝试上一行(或多行)的其他摆法是否可行. 那是否可行呢? 当然还是通过向下递归来判断的. 如果又发生了向上回退, 则需要再次尝试上一行(或多行)的其他摆放方式, 以此类推.
向上回退的情形2: 找到了一组解
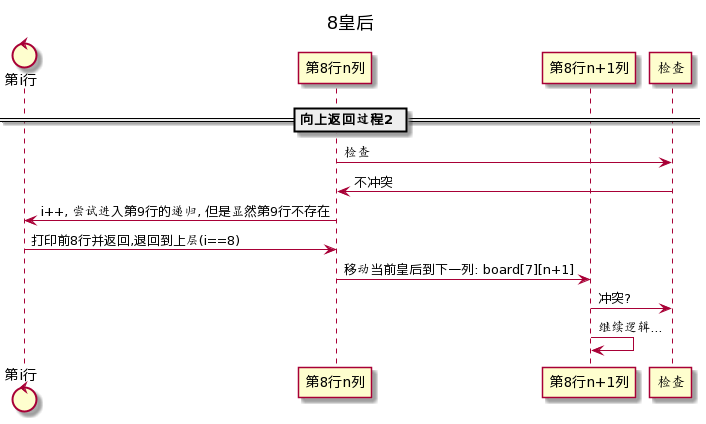
其实写完了uml发现解释的还是挺复杂的, 并没有比原文小哥搞得更清晰. 不过主流程提炼了一波, 会好一些, 下面就给出Golang实现的代码:
package main
import (
"fmt"
)
func main() {
// init cheese board
board := make([][]int, 8)
for i := range board {
board[i] = make([]int, 8)
}
fmt.Println("init board.. ")
printBoard(board)
// put first queen
findQueen(board, 0)
}
var count int
func findQueen(board [][]int, row int) {
// print when succeed
if row == len(board) {
count++
fmt.Println("found success", "count: ", count)
printBoard(board)
return
}
// loop board col
for j := 0; j < len(board[0]); j++ {
// try put queen
board[row][j] = 1
if !checkValid(board, row, j) {
board[row][j] = 0
continue
}
findQueen(board, row+1)
// revert this step try another options
board[row][j] = 0
}
}
func checkValid(board [][]int, row, col int) bool {
// horizon, vertical, diagonal, back diagonal
var h, v, d, bd int
// horzion
for i := 0; i < len(board); i++ {
if board[row][i] == 1 {
h++
}
}
// vertical
for i := 0; i < len(board[0]); i++ {
if board[i][col] == 1 {
v++
}
}
// diagonal func: f(x) == -x + b, given point(row, col)
// col == -row + b
// b == col + row
b := col + row
// i means x as row, -i+b means y as col
for i := 0; i < len(board); i++ {
if -i+b >= 0 && -i+b < len(board[0]) && board[i][-i+b] == 1 {
d++
}
}
// back diagonal func : f(x) == x + b, given pot(row, col)
// col = row + b
// b = col - row
bb := col - row
for i := 0; i < len(board); i++ {
if i+bb >= 0 && i+bb < len(board[0]) && board[i][i+bb] == 1 {
bd++
}
}
if h == 1 && v == h && d == h && bd == h {
return true
}
return false
}
func printBoard(board [][]int) {
for _, v := range board {
fmt.Printf("%v \n", v)
}
}
这里其实还可以解释一下checkValid()方法, 这个方法就是判断某个点的米字型范围是否有其他的点, 我参考了直线方程:f(x)=kx+b, 然后判断了一下主副对角线上有没有多余的点的值等于1. 合法条件下横竖撇捺任何方向的点加起来的值各都是1.
附件: plantuml 源文件
@startuml
title "8皇后"
control 第i行
participant 第1列
participant 第2列
participant 第3列
participant 第...列
participant 检查
== 向下递归过程 ==
第i行 -> 第i行: (从0 到 7 行)
第i行 -> 第1列: i:= 0; 尝试放到board[0][0]
第1列 -> 检查: 是否米字型冲突
检查 -> 第1列: 不冲突
第1列 -> 第i行: i++, 向下一行递归
第i行 -> 第1列: i == 1; 尝试放到board[1][0]
第1列 -> 检查: 检查
检查 -> 第1列: 冲突
第1列 -> 第2列: 尝试将该行皇后移动到第二列 board[1][1]
第2列 -> 检查: 检查
检查 -> 第2列: 冲突
第2列 -> 第3列: 移动到第三列 board[1][2]
第3列 -> 检查: 检查
检查 -> 第3列: 不冲突
第3列 -> 第...列: 依次向后board[1][...]
== ==
@enduml
@startuml
title "8皇后"
control 第i行
participant "第n+1列"
participant 第8列
participant 检查
== 向上返回过程1 ==
第8列 -> 检查: 检查
检查 -> 第8列: 冲突, 此时当前行不论皇后放哪一列都冲突. 同时说明之前行的摆放不足以完成后继匹配, 需要逐层回溯找其他摆法.
第8列 -> 第8列: 清空摆放 board[i+1][7] = 0 // 当前所在第i+1行
第8列 -> 第i行: 递归return, 回到上一行, 即第i行
第i行 -> "第n+1列": 第i行原本board[i][n]的皇后,向后移动一位: board[i][n+1]
"第n+1列" -> 检查: 检查
检查 -> "第n+1列": 冲突?
"第n+1列" -> "第n+1列": 继续向下或者向上递归...
== ==
@enduml
@startuml
title "8皇后"
control 第i行
participant 第8行n列
participant "第8行n+1列"
participant 检查
== 向上返回过程2 ==
第8行n列 -> 检查: 检查
检查 -> 第8行n列: 不冲突
第8行n列 -> 第i行: i++, 尝试进入第9行的递归, 但是显然第9行不存在
第i行 -> 第8行n列: 打印前8行并返回,退回到上层(i==8)
第8行n列 -> "第8行n+1列": 移动当前皇后到下一列: board[7][n+1]
"第8行n+1列" -> 检查: 冲突?
"第8行n+1列" -> "第8行n+1列": 继续逻辑...
@enduml